Fizika-alapú kovariancia-függvény rezgőrendszerek Gauss-folyamat alapú állapotbecslésére
Témavezető
Sykora Henrik
Email
sykora@mm.bme.hu
Típus
BSc MSc TDK
Nyelv
magyar angol
Bevezető:
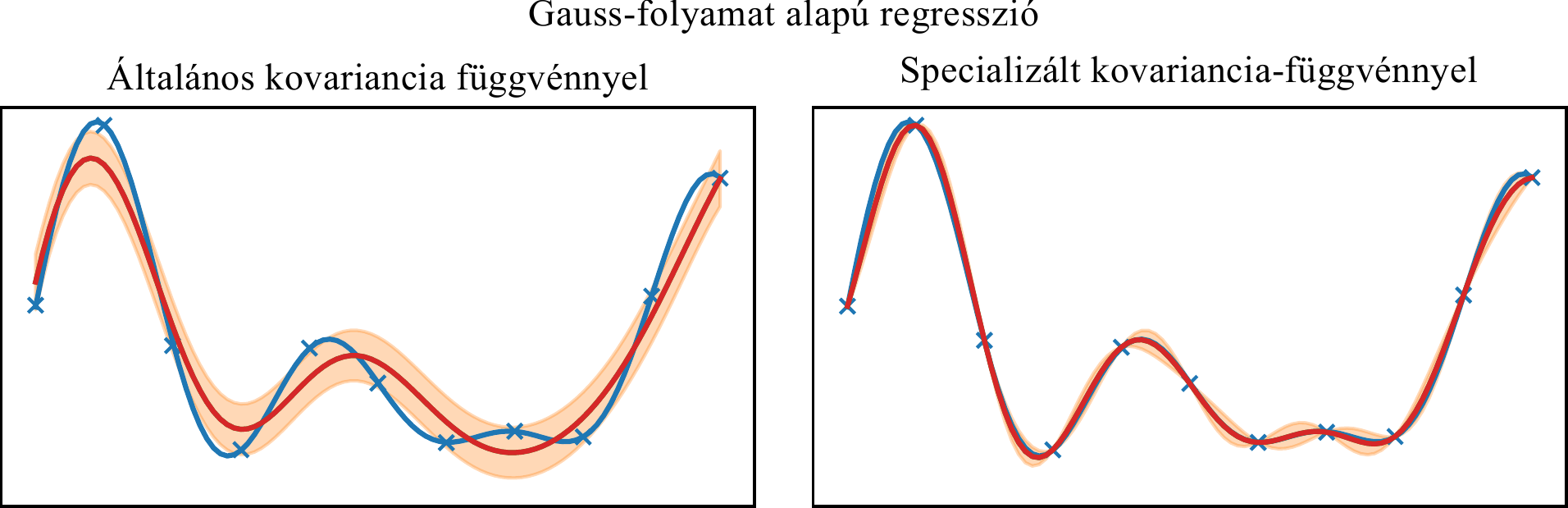
A Gauss-folymat alapú regresszió a gépi tanulás egy népszerű eszköze. A módszer elsősorban statisztikai alapokon nyugszik, és a mérési pontok közötti kovarianciát felhasználva becsli az ismeretlen függvényértékeket. Szükség esetén mérési zajszűrés, illetve eredeztetett mennyiségek (pl deriváltak) becslésére is alkalmas, annak bizonytalanságának becslésével együtt. Fizikai rendszereken végzett mérések esetén a regresszió pontossága és megbízhatósága jelentősen növelhető, ha a fizikai rendszer viselkedését figyelembe vevő kovariancia-függvényt használunk a regresszió során. A dolgozat célja különböző rezgőrendszerekre specializált kovariancia-függvények kidolgozása, majd szimulált/mért adatokon regresszió végzése, kovariancia-függvények regressziós teljesítményének összehasonlítása.Feladatok:
- Irodalomkutatás Gauss-folymatokkal végzett regresszió témakörében- Rezgőrendszerekre specializált kovariancia-függvények létrehozása
- Gauss-folymat regresszió pontosságának vizsgálata különböző kovariancia-függvények esetén
A projekt kidolgozása során az alábbi, kerettantervben nem szereplő, vagy csak röviden érintett jártasságok szerezhetőek, elmélyíthetőek:
- Gauss-folyamat alkalmazása, fejlesztése
- Rezgőrendszerek paramétereinek és nem mért állapotváltozóinak adatvezérelt illesztése és becslése
- Korszerű statisztikai és gépi tanulási módszerek alkalmazása
- Nagy teljesítményigényű számítások programozása