Predicting Global Bifurcations in Dynamical Systems using Neural Networks
Témavezető
Habib Giuseppe
Email
habib@mm.bme.hu
Típus
BSc MSc TDK
Nyelv
magyar angol
Bevezető:
Steady-state solutions of dynamical systems, such as fixed points, periodic solutions, and more complex quasiperiodic and chaotic motions, have been widely studied in the literature. While methods exist for studying the stability of fixed points and periodic solutions, including predicting bifurcations through the variation of system's eigenvalues or Floquet multipliers, it is much more challenging to predict global bifurcations – changes in the topology of the system's phase space – due to the lack of a formalized approach. However, it is possible to recognize signs that a system is approaching a global bifurcation by observing its trajectories in the phase space.The goal of this thesis is to use neural networks to predict global bifurcations in dynamical systems based on a small number of phase space trajectories.
Feladatok:
- Conduct a literature review on global bifurcation detection and prediction techniques- Select a specific bifurcation to be analyzed
- Using existing systems from the literature, generate phase space trajectories that correspond to a known global bifurcation occurring at a specific parameter value
- Simplify and organize the collected data for use in training a neural network
- Experiment with different neural network architectures for the prediction task
- Train and test the various networks
- Compare the results and draw conclusions
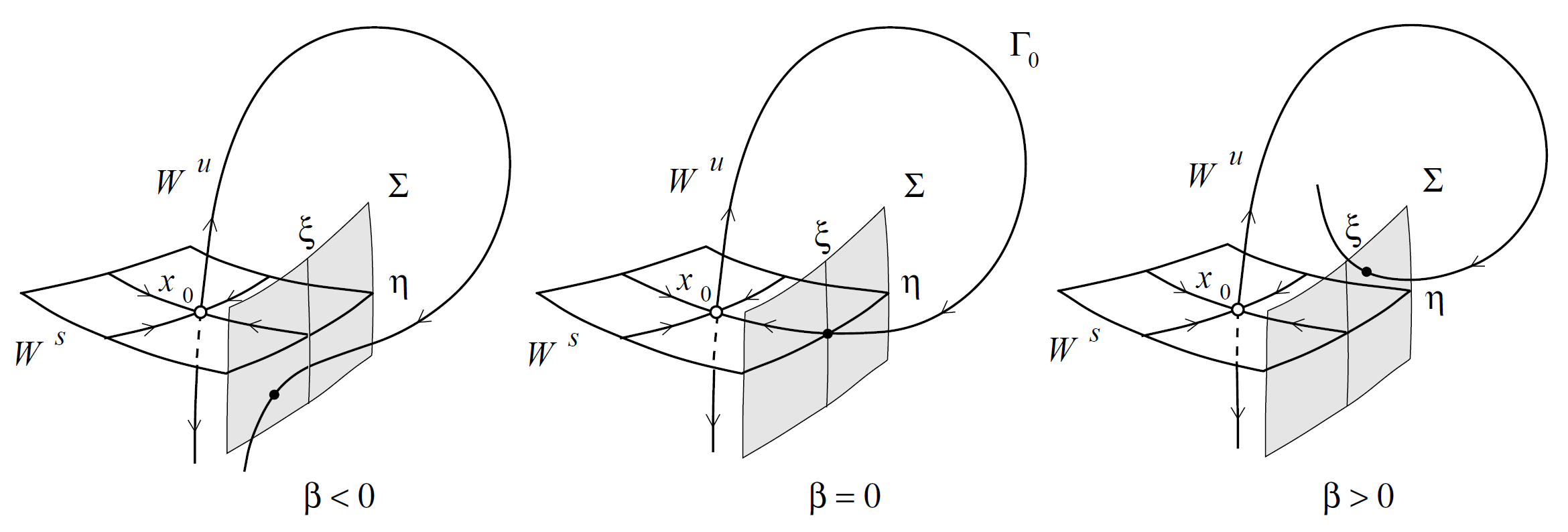
Example of global dynamics topology change through a homoclinic orbit (from Kuznetsov - Elements of applied bifurcation theory)

